A subtly wrong proof that ChatGPT generated

Let the matrix $C$ be the second moment of the vector $\text{relu}(z)$, where $z$ follows a multivariate normal distribution $\mathcal{N}(0, K)$ with $K$ being the covariance matrix. For two normal distributions, does $K_1 \succeq K_2$ imply $C_1 \succeq C_2$?

This question originated from our research on understanding the training dynamics of graph neural networks under neighborhood sampling (e.g., FastGCN). The continuous analog of neural network training is a gradient flow, which admits a closed-form solution characterized by the covariance matrix of the network outputs before training and the Gram matrix (kernel matrix) of the network gradient during training. Both the covariance matrix and the kernel matrix can be recursively computed in a closed form, layer-by-layer. Hence, we use $K$ to denote the covariance matrix of the layer, as well as the final network, outputs without confusion. The matrix $C$ is a quantity between the two $K$’s in two consecutive layers. For training graph neural networks, neighborhood sampling incurs approximations to $K$. We intended to explore if the approximation was a shrinkage. Because of the recursive nature of the computation of $K$, if there were indeed shrinkage, a natural way to prove so was by mathematical induction, beginning from the input layer and extending to the output layer. That is where the initial question came from.

However tempting a positive answer to the question looks, I struggled to prove it. I turned to ChatGPT for some hints. It was a while ago but I still have its proof. The proof looked mathematically fluent, except that it was flawed. In fact, not just the proof was wrong, the claim that “$K_1 \succeq K_2$ implies $C_1 \succeq C_2$” was wrong.

To be fair, at the time of writing this post, I try ChatGPT again and it asserts correctly: $K_1 \succeq K_2$ does not imply $C_1 \succeq C_2$. There could be many reasons for the inconsistency. ChatGPT might have improved over the past few months. It might learn from the counterexample that we gave in our preprint. It might be affected by how I prompted it — it produced a wrong proof when I asked it to prove that K_1 > K_2 implies C_1 > C_2, while it made the correct assertion when I asked does K_1 > K_2 imply C_1 > C_2? Moreover, the inconsistency might even be just the stochastic nature of generative AI — you get a different answer if the sampling temperature is nonzero.

I am not to make a negative point of ChatGPT or other AI tools here. In fact, I like them because they truly help me improve my productivity in work and life. The message I want to say is

It takes a mathematician to verify the mathematical content generated by AI.

---

Here is how the mathematically fluent, but wrong, proof goes. A saved ChatGPT conversation can be found here.

Define the notation $C(K) := \mathbb{E}[ \, \text{relu}(z) \, \text{relu}(z)^T \, ]$. The objective is to show that $C(K_1) \succeq C(K_2)$ when $K_1 \succeq K_2$. To this end, we define the quadratic form $F(K) := v^T C(K) v = \mathbb{E}[( v^T \text{relu}(z) )^2]$ for any test vector $v$ and the interpolation $K(t) := K_2 + tH$ where $H := K_1 - K_2 \succeq 0$. It suffices to show that $F(K(t))$ is nondecreasing in $t$ on $[0,1]$.

Because relu is nonsmooth at the origin, we use a smooth and convex surrogate $\phi_{\epsilon}$ (e.g., softplus) such that

\[\phi_{\epsilon} \to \text{relu}, \quad \phi'_{\epsilon} \to 1_{\{x>0\}}, \quad\text{and}\quad \phi''_{\epsilon} \ge 0, \quad\text{when}\quad \epsilon \to 0.\]

Then, define $F_{\epsilon}(K) = \mathbb{E}[( v^T \phi_{\epsilon}(z) )^2]$. For smooth $f$, Price’s theorem (Gaussian differentiation formula) gives

\[\frac{d}{dt} F_{\epsilon}(K(t)) = \frac{1}{2} \mathbb{E}[\text{tr}(H \nabla^2 f(z))], \quad f(z) = s(z)^2, \quad s(z) = v^T\phi_{\epsilon}(z).\]

A direct computation yields

\[\nabla^2 f(z) = 2 (\nabla s)(\nabla s)^T + 2s(z) \text{diag}\left( v_i \phi''_{\epsilon}(z_i) \right).\]

Hence,

\[\text{tr}(H \nabla^2 f(z)) = 2(\nabla s)^T H (\nabla s) + 2 s(z) \sum_i H_{ii} v_i \phi''_{\epsilon}(z_i).\]

• The first term is nonnegative since $H \succeq 0$.
• The second term vanishes in expectation as $\epsilon\to0$, because $\phi_{\epsilon}’’$ concentrates near 0 while Gaussian mass there goes to zero.

Therefore, taking limits, $\frac{d}{dt} F(K(t)) \ge 0$ for all $t$. Then, integrating from $t=0$ to $t=1$, we have

\[F(K_1) - F(K_2) = \int_0^1 \frac{d}{dt} F(K(t)) \, dt \ge 0,\]

which proves that $C(K_1) - C(K_2) \succeq 0$.

---

Notice what’s wrong? I would say the proof strategy is clever: it leverages the monotonicity of Gaussian expectations of convex functions. The proof would have been correct for an activation function that is both smooth and convex. The problem for relu lies in its nonsmoothness at the origin.

The flaw of the proof appears in the second bullet point: $\phi_{\epsilon}’’$ concentrates near 0 but the Gaussian mass there is nonzero. For relu, its first derivative has a discontinuity at 0, which makes its second derivative a Dirac delta function. The surrogate $\phi_{\epsilon}’’$ converges to the Dirac delta in distribution, which makes $\mathbb{E} [ s(z) \sum_i H_{ii} v_i \phi_{\epsilon}’’ ]$ nonzero. The expectation could be either positive or negative, forfeiting the positivity of $\frac{d}{dt} F_{\epsilon}(K(t))$.

---

At the time of writing this post, I prompt ChatGPT by asking it whether K_1 > K_2 implies C_1 > C_2? ChatGPT makes it right this time by saying no. It also gives an elegant example:

\[K_2 = \begin{bmatrix} 1 & \rho \\ \rho & 1 \end{bmatrix}, \quad K_1 = \begin{bmatrix} 1 + \epsilon & 0 \\ 0 & 1 + \epsilon \end{bmatrix},\]

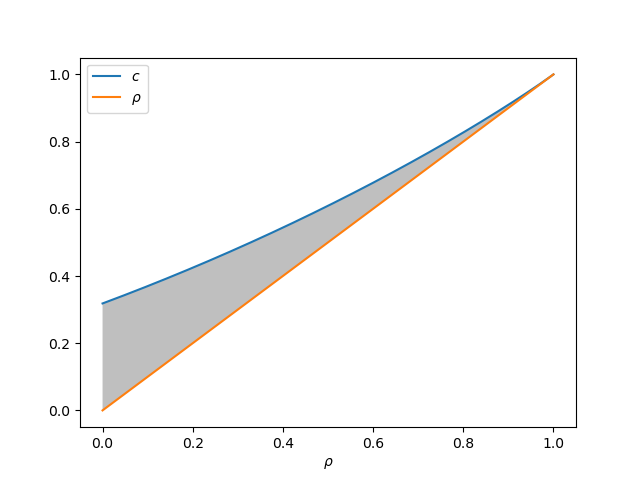
where $\rho \in (0,1)$ and $\epsilon \ge \rho$. Using the formulas from Appendix C of my paper, we obtain

\[C_2 = \frac{1}{2} \begin{bmatrix} 1 & c \\ c & 1 \end{bmatrix}, \quad C_1 = \frac{1}{2} \begin{bmatrix} 1+\epsilon & 0 \\ 0 & 1+\epsilon \end{bmatrix}, \quad c = \frac{1}{\pi} \left( \sqrt{1-\rho^2} + \rho (\pi - \arccos\rho) \right).\]

Then,

\[C_1 - C_2 = \frac{1}{2} \begin{bmatrix} \epsilon & -c \\ -c & \epsilon \end{bmatrix}.\]

For any $\epsilon \in [\rho, c]$, we have $C_1 \preceq C_2$ rather than $C_1 \succeq C_2$. The shaded region in the plot below indicates such a choice of $\epsilon$.